I am an experimentalist working with light. I do nonlinear and quantum optics experiments. Nowadays, my favorite system is microcavity exciton-polaritons, with which I create quantum fluids of light and address exciting basic physics topics ranging from many-body phenomena to quantum information processing.
A new spectroscopy method
At LKB, we have developed a new, high-resolution spectroscopy method that allows us to to observe collective excitations in quantum fluids of light. Differently from previous measurement techniques, our pump-probe method allows us to resolve the spectrum at all angles, by filtering out light from the mean-field. This is the basic tool that has enabled all my research in polaritons.
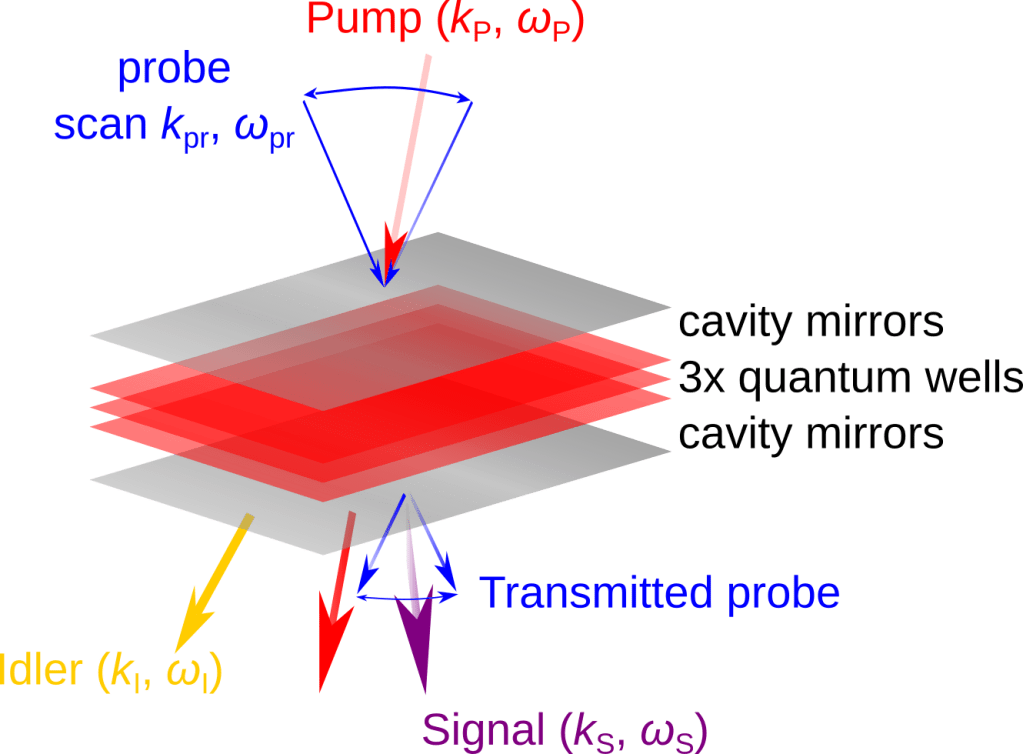
Paper describing the method: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.103601
We have used the method to study the spectrum when the cavity is excited near resonance with the bottom of the polariton branch: https://journals.aps.org/prb/abstract/10.1103/PhysRevB.107.174507
Phase transitions out of equilibrium
Symmetry is one of the great unifying themes in physics. From cosmology to nuclear physics and from soft matter to quantum materials, symmetries determine which interactions and evolutions occur in nature.
Experiments with ultra-cold atoms have evidenced that spontaneous symmetry breaking across the BEC transition at
equilibrium is associated with propagating Nambu-Goldstone modes – equilibrium BECs are superfluids.
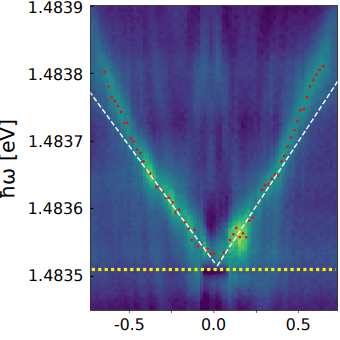
However, most physical systems in Nature are not in thermal equilibrium and the Nambu-Goldstone mode is then non-propagative. Instead, excitations relax according to a diffusion equation – BECs out of thermal equilibrium are not superfluids and I have shown this in an experiment in 2023: https://arxiv.org/abs/2310.11903

If however we excite the microcavity such that the phase of the fluid of light is fixed, a superfluid can form!
Analogue quantum simulation of quantum field theory in curved spacetime
The quantum dynamics of fields is a frontier in our physical models for condensed matter, high energy physics and black holes. A key signature of these dynamics is the generation of entanglement.
Recent calculations (by my collaborators at Louisiana State Univ https://journals.aps.org/prd/abstract/10.1103/PhysRevD.110.025021) based on Gaussian states permit to quantitatively assess the entanglement generated by black holes
and its modification by the Hawking-superradiance interplay. However, these new predictions of QFTCS cannot be tested in the relativistic context because the interior of the black hole is inaccessible and the signal going away from it is too weak.
Fortunately, new developments in laboratory experiments enable the study of quantum fields in controlled systems. In the lab, we create experimental models of quantum fields on curved spacetimes, simulating rotating or non-rotating black hole and measure the dynamics of entanglement.
Check out the experiment on the simulation of QFTCS in the Schwarzschild (non-rotating) geometry! https://arxiv.org/abs/2311.01392
In the experiment, the effectively curved spacetime is realised with the meanfield of the fluid of light. A rotating black hole geometry can be created by coherent pumping with a Laguerre-Gauss beam, creating a giant (multiply charged) polariton vortex. Meanwhile, the quantum field is modelled by the fluid’s collective excitations whose wave equation is formally equivalent to a Klein-Gordon field on a curved spacetime.
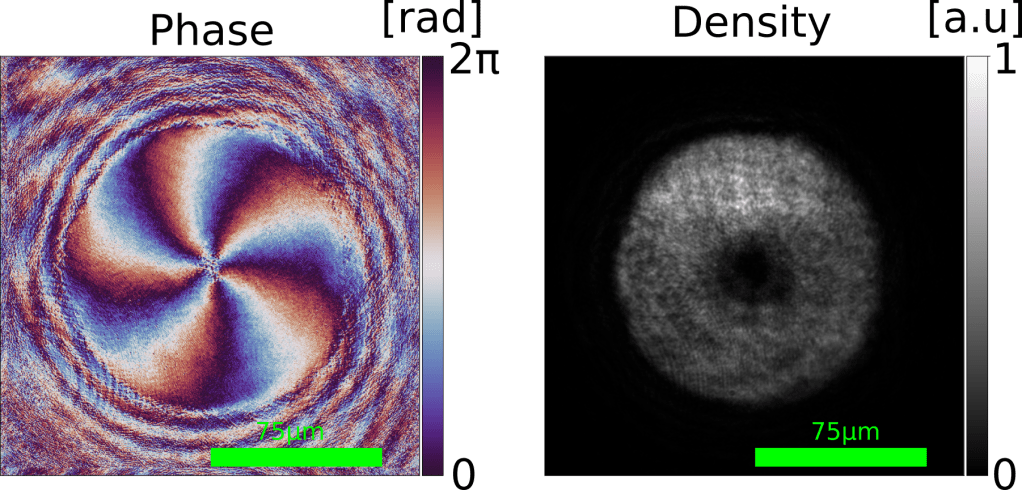
Quantum field theory in curved spacetime
In order to guide the experiments, I have developed an analytical theory of QFTCS in optical systems, and a new numerical code based on the Truncated Wigner approximation to simulate the quantum dynamics of polariton fluids in a variety of geometries.
With my collaborators at LSU, we have shown for the first time that superradiance amplifies vacuum fluctuations to yield entangled pairs, and also that entanglement at the output can be increased by using squeezed states at the input.
In 2023, I discovered a new effect of QFTCS: if there are unstable trajectories near acoustic horizons, vacuum fluctuations will perturb the horizon. This leads to the emission of quasi-normal modes (resonances) of the quantum field. These QNMs will leave their imprints on the Hawking spectrum, which is means that observing the spectrum gives information on the near horizon geometry! I tell you all about this in a youtube video here https://www.youtube.com/watch?v=hR5Nho3DhR8!